Strength In Numbers: Using Regression for Pay Equity Analyses
January 26, 2018 •Shane Thompson

In the next post of our blog series on how statistics can be useful in litigation cases, Dr. Shane Thompson discusses how regression can be a powerful tool in pay equity cases.
In our first post of this series, we discussed how evidence in the courtroom is becoming more and more quantitative. Correspondingly, statistical and regression models are vital tools for presenting evidence. In this post, we discuss the power and necessity of regression using a specific example: pay equity analysis.
Pay equity analyses need regression to isolate the drivers of pay (in)equity. With descriptive employee data at our disposal and an appropriate statistical model, we can separate the influence of gender, race, or age on salary while simultaneously accounting for other potential contributors.
Suppose, for example, that in company data we observe higher average salaries for male employees. Is this, on its own, evidence of wage discrimination? Not necessarily, because our analysis has not yet accounted for other differences that might exist between male and female employees.
As we examine the (hypothetical) data further, we may uncover that male employees are, on average, more qualified than their female counterparts at the company. Suppose that:
- Male employees have more average experience than female employees
- More male employees work at a branch of the company in an expensive metropolitan area
- A higher proportion of male employees have master’s degrees than female employees
- A higher proportion of male employees work in high-tech positions than female employees
If this is the case, we would expect male employees to have higher salaries than female employees based on qualifications, not gender. The figure below highlights how statistical models separate a true effect of gender from other effects.
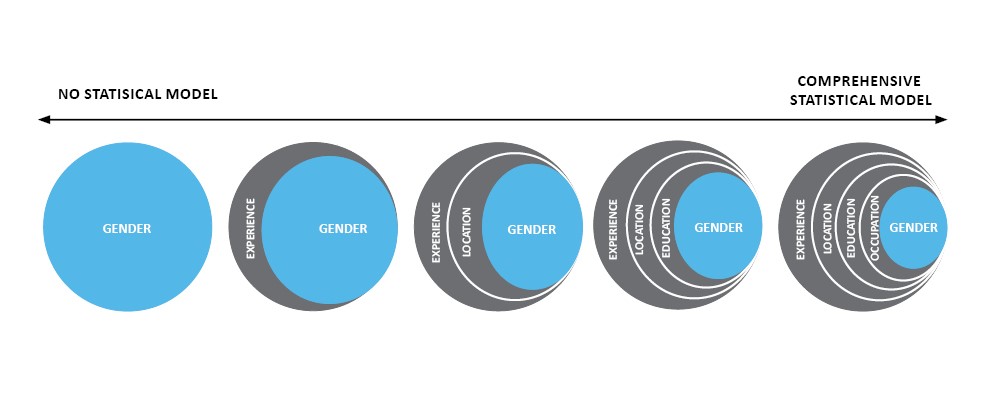
The first large, blue circle represents the raw difference in the salary between male and female salaries before accounting for other factors. As we add factors to our model, we see that the original differential, which we may have naively attributed solely to gender, is also driven by experience, location, education, and occupation. Once we account for these additional factors, the amount of the differential directly attributable to gender has diminished substantially. Because we have a statistical model, we can determine whether the diminished effect of gender is statistically different from zero, i.e., whether there is indeed statistical evidence of gender pay inequity after accounting for all other factors.
In summary, a comprehensive regression model produces two things raw data cannot: first, an estimate of gender pay inequity that simultaneously accounts for other relevant factors; and second, a determination whether that estimate is statistically significantly different from zero.
Note: In the hypothetical example above, gender pay inequity was non-existent after removing the influence of other factors. However, in some cases when gender pay inequity is present, accounting for the influence of other factors may actually increase the effect of gender from its raw starting point (the first blue dot). Statistical models have no innate bias in any one direction.
Get Updates
Featured Articles
Categories
- affordable housing (12)
- agile (3)
- AI (4)
- budget (3)
- change management (1)
- climate resilience (5)
- cloud computing (2)
- company announcements (15)
- consumer protection (3)
- COVID-19 (7)
- data analytics (82)
- data science (1)
- executive branch (4)
- fair lending (13)
- federal credit (36)
- federal finance (7)
- federal loans (7)
- federal register (2)
- financial institutions (1)
- Form 5500 (5)
- grants (1)
- healthcare (17)
- impact investing (12)
- infrastructure (13)
- LIBOR (4)
- litigation (8)
- machine learning (2)
- mechanical turk (3)
- mission-oriented finance (7)
- modeling (9)
- mortgage finance (10)
- office culture (26)
- opioid crisis (5)
- Opportunity Finance Network (4)
- opportunity zones (12)
- partnership (15)
- pay equity (5)
- predictive analytics (15)
- press coverage (3)
- program and business modernization (7)
- program evaluation (29)
- racial and social justice (8)
- real estate (2)
- risk management (10)
- rural communities (9)
- series - loan monitoring and AI (4)
- series - transforming federal lending (3)
- strength in numbers series (9)
- summer interns (7)
- taxes (7)
- thought leadership (4)
- white paper (15)


