Strength In Numbers: Sampling, A Powerful Tool in Expert Hands
February 9, 2018 •Balint Peto

In the third post of this series, we show how statistical sampling could provide accurate and precise quantitative evidence cost effectively. You can find the rest of the Strength In Numbers blog posts here.
A statistical sample is a small subset of a larger population. Selected properly, a statistical sample allows for drawing valid conclusions about that population. For example, public opinion polls are used to draw conclusions about the opinions of the general public by only asking a randomly selected sample of respondents.
The key to a valid sample is a simple principle: each member of the population has a known and non-zero chance to be included. The purpose of this blog is to unpack this seemingly simple principle.
Advantages of Sampling: Working Smarter, Not Harder
Because a sample (say, in the hundreds) can be much smaller than a population (in the hundreds of millions), it is much more cost effective to evaluate a sample than the population. Surprisingly, with a very large population, such as the population of the United States (about 320 million), it takes a very small sample (about 1,000) to achieve reliable conclusions. (See our previous blog post on sampling myths).
There are multiple ways to select a valid statistical sample. For example, a lottery is a statistically valid simple random sample. In a lottery, every ball has the same chance to be selected. Because of its simplicity, this is called a simple random sample. But a lottery is not the only way to selecting a sample. An alternative to a lottery is to create groups within a population before samples are selected from the groups. Frequently, groups are created based on similarity (say, groups of men or women). The latter is a stratified sample.
This similarity will allow for selecting even fewer elements from each group and still get reliable conclusions about the population. However, the subject matter expertise and the sampling expertise are both essential to (1) identify the groups that are similar, and to (2) select the appropriate number of elements from each group. [1]
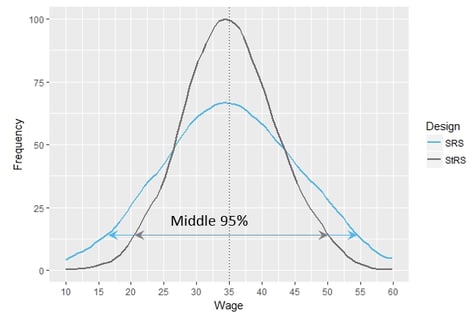
The graphic on the right compares wage estimates from a large number of simple random samples (SRS) to wage estimates from a large number of stratified random samples (StRS) of the same size, all drawn from the same population. As the graphs show, the StRS is similar to SRS with respect to the average estimated wage, about 35. However, estimates from the stratified samples are more likely to be nearer the center. As shown in the graphic, 95% of SRS sample (blue line) averages fall between 15.5 and 54.5, while 95% of StRS sample (black line) averages fall between 21 and 49.7, which makes the StRS estimates more precise.
In this previous blog post, we discussed the details of simple random sampling and some other designs.
Case Studies: Applying Theoretical and Industry Expertise
At Summit, we pair subject matter experts with statisticians to serve our clients.
For example, we helped the U.S. Department of Labor measure the extent of civil infractions among the 700,000 entities that file Form 5500 annually. For this project, Summit helped design a series of samples that use the information about retirement plan types and the number of retirement plan participants to create groups. By selecting a sample of a few hundred retirement plans, we achieved a reliable estimate of the rate of civil infractions. (In a future blog post we will discuss why the reported rate of civil infractions via investigations is an unreliable measure of the baseline. See details here.)
Quantifying the extent of fraudulent activities among claims is another example of leveraging information to improve sample design. In other projects, we used claim types to create groups (strata), taking advantage of the fact that claims are similar to each other within certain claim types but different from each other across those claim types. Further, we often create a separate group for claims with an amount greater than a certain large value to make sure those large claims are all included in the sample.
Conclusion
Statistical sampling can be a very powerful tool in the right hands. Selecting a sample may appear straightforward, but there are many pitfalls--careful statistical and subject matter considerations are needed to make sure the sample is both statistically valid and efficient.
[1] In stratification, the similarity within strata is only important with respect to the outcome of interest. For example, if we want to measure body heights, it is probably a good idea to group by gender, because women’s and men’s heights are generally likely to be different across those two groups, but similar within. However, if we are interested in some other metric, such the average daily commute time, we are probably better off looking for other grouping variables, such as urban, suburban, or rural residence.
Get Updates
Featured Articles
Categories
- affordable housing (12)
- agile (3)
- AI (4)
- budget (3)
- change management (1)
- climate resilience (5)
- cloud computing (2)
- company announcements (15)
- consumer protection (3)
- COVID-19 (7)
- data analytics (82)
- data science (1)
- executive branch (4)
- fair lending (13)
- federal credit (36)
- federal finance (7)
- federal loans (7)
- federal register (2)
- financial institutions (1)
- Form 5500 (5)
- grants (1)
- healthcare (17)
- impact investing (12)
- infrastructure (13)
- LIBOR (4)
- litigation (8)
- machine learning (2)
- mechanical turk (3)
- mission-oriented finance (7)
- modeling (9)
- mortgage finance (10)
- office culture (26)
- opioid crisis (5)
- Opportunity Finance Network (4)
- opportunity zones (12)
- partnership (15)
- pay equity (5)
- predictive analytics (15)
- press coverage (3)
- program and business modernization (7)
- program evaluation (29)
- racial and social justice (8)
- real estate (2)
- risk management (10)
- rural communities (9)
- series - loan monitoring and AI (4)
- series - transforming federal lending (3)
- strength in numbers series (9)
- summer interns (7)
- taxes (7)
- thought leadership (4)
- white paper (15)


