August 7, 2015 •Melissa Cichantek
* Welcome to the third post in Summit's 2015 Summer Intern Series! See below for Summer Analyst Adam Banker’s essay. Click here to learn more about our Summer Analyst/Associate program. *
Let us start out with a hypothetical scenario: suppose that you are a salesperson. You work for a data company (Congratulations! I hear the field is booming) and starting Monday, you will embark on a cross-country, multi-city sales trip. While you enjoy the boardroom bustle of Manhattan and the arm twisting in Dallas, you need to be back home before your tennis match back home on Saturday. Therefore, you have one main thought before you leave: what is the shortest travel route that will take you to all of your client sites then back home by the weekend?
For a human, finding the quickest route between a few places is quite simple. You would grab a map, locate your destinations, and then simply draw a path that looks the “most direct” to you. Finding the solution is for a handful of destinations is easy because people have an inherent understanding of what “most direct” means (e.g., no zig-zagging).
But let’s now say that your trip was extended to include 50 cities (goodbye tennis match) or that you have been promoted to plan everyone else’s routes as well. In this case, it would make sense to have a computer determine trip routes for you. Unfortunately, computers have no innate understanding of “most direct,” so you must create that ability.
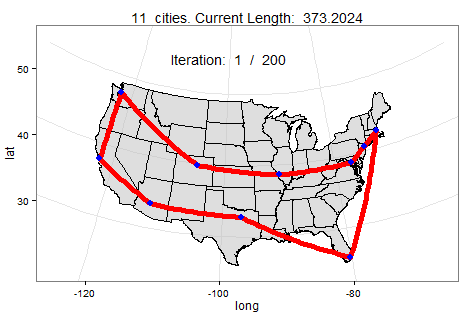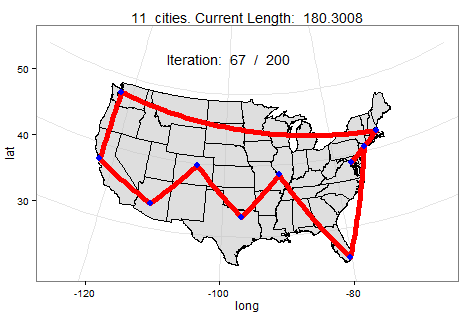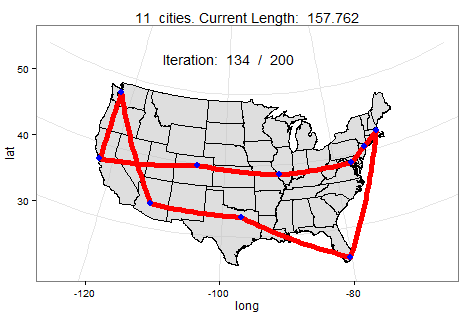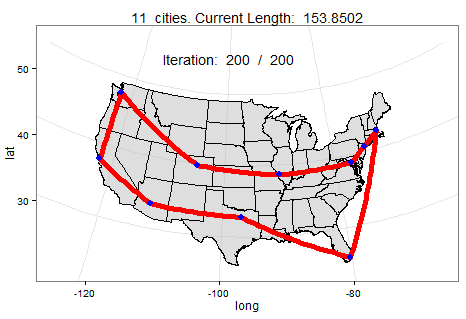
A computer can plan the shortest route using a probabilistic method called simulated annealing, which is like a smart guess-and-check. To start, it picks any random path between your clients regardless of how unreasonable it may seem. Then, it will mutate the original path by reversing when you visit two of your clients. So let’s say that in your original path, you were set to make your second stop in Seattle and your fourth stop in Denver. In the mutated path, the computer pushes up your meeting in Denver to be the second stop and move back Seattle to fourth. While those two stops flip, every other stop in the two paths remains the same. If the new mutated path is shorter, the computer keeps it. If the mutated path is longer, however, it determines whether to keep the original or mutated path by flipping a coin. It may appear strange to keep a path that is worse, but keeping longer paths is necessary since the absolute best path may be a closer mutation of what is currently a worse path.
Below we can watch a slowed-down animation of how a computer found the best roundtrip path between 10 cities. In this scenario, the computer found the shortest path in under 200 mutations (i.e., faster than you could pick up a pen to draw your own route).
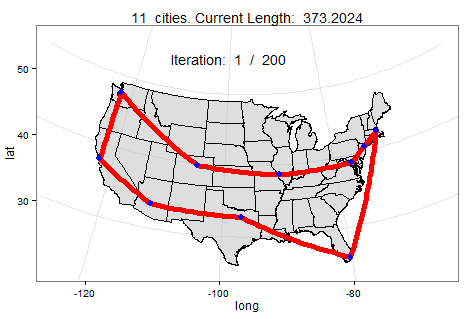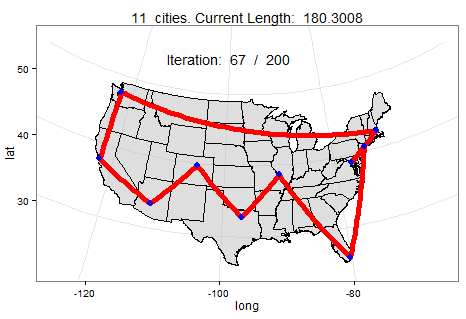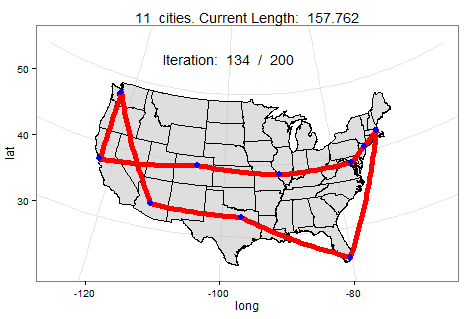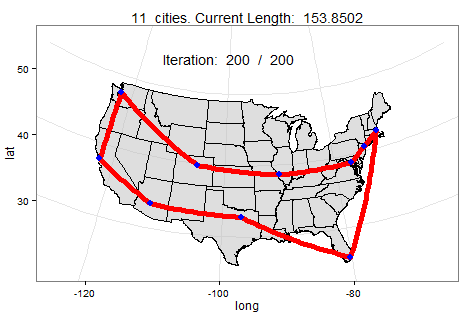
What makes simulated annealing appealing is that it can be used for so much more than finding a shortest path. Check out this GitHub page for more simulated annealing ideas. If you plan to experiment with simulated annealing on a different problem, let me know how it goes in the comments!